_

1. 소개

펜윅 트리는 구간 트리의 한 종류다. 주로 구간 합을 빠르게 구할 때 사용되고 BIT(Binary Indexed Tree)라고도 불린다. 펜윅 트리는 기존의 구간 합을 구할 때 사용하였던 구간 트리인 Segment Tree 등에서 미리 계산하여 저장한 정보들 중 많은 양의 정보가 실제로 필요하지 않다는 점을 이용한다.

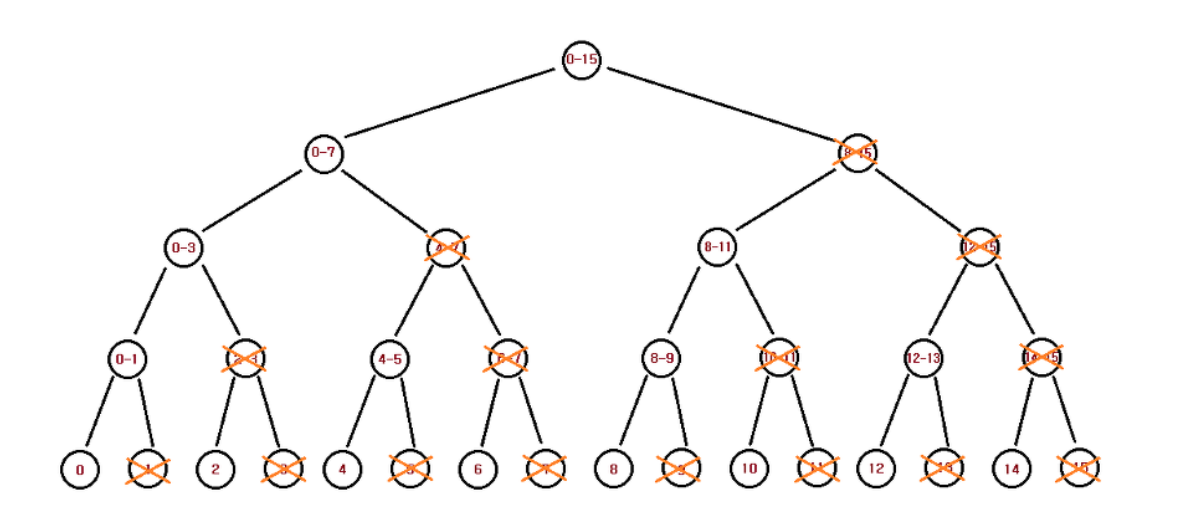
부분 합(1번째 원소부터의 합)을 구할 때 필요한 정보들만을 계산하여 부분 합을 구하여 s부터 e까지의 구간 합을 계산한다고 하면 e까지의 부분 합에서 s-1까지의 부분 합을 빼서 구간 합을 구할 수 있다. 따라서 Segment Tree에서 모든 구간 노드에 대해 각 노드의 오른쪽 자식은 필요로 하지 않는다¹ . 필요 없는 정보들이 차지한 공간을 제외하여 만든 펜윅 트리는 다음 그림과 같다.

2. Code

Fenwick Tree에서 구간 노드들 간 이동을 할 때 각 구간 노드들의 번호를 이진수로 표현한 것을 사용한다.

Update 연산을 해주는 경우 i번째 구간 노드에 업데이트 해준 다음 (i + (i & -i) )번째 노드로 이동하여 업데이트를 해준다. 이 과정을 \(i\)가 Fenwick Tree에 저장한 원소 개수 \(N\)을 넘지 않는 동안 반복한다.

구간 합 Fenwick Tree를 예로 들면, Sum 연산에서는 \(1\)번째 원소부터 \(i\)번째 원소 까지 합을 구한다. 이는 i번째 구간 노드의 합을 더한 다음 i - (i & -i) )번째 노드로 이동하여 구간 노드의 합을 더해주는 과정을 Update 연산과 비슷하게 \(i>0\)인 동안 반복하여 처리할 수 있다.

int fenwick_tree[MAX_N+1];

void Update(int x, int y){ // x번째 원소가 y만큼 증가함
	while(x<=N){
		fenwick_tree[x] += y;
		x = x + (x & -x);
	}
}

int Sum(int x){	// 1부터 x번째 까지 합
	int sum = 0;
	while(x>0){	
		sum += fenwick_tree[x];
		x = x - (x & -x);
	}
}

Update와 Sum 연산 모두 \(O(\log N)\)의 시간복잡도를 갖는다.

3. 구간 더하기

Fenwick Tree에서 다음과 같은 연산도 할 수 있다.

\(x\)부터 \(y\)까지 \(z\)만큼 더한다.
\(x\)번째 원소의 값을 구한다.

\(i\)번째 원소를 \(a_i\)라 하고 Fenwick Tree \(i\)번째 위치에 \(a_i - a_{i-1}\)을 저장하는 구간 합 Fenwick Tree를 만든다고 생각해보자. \(x\)부터 \(y\)까지 \(z\)만큼 더하는 것은 \(a_x - a_{x-1}\)가 \(z\)만큼 증가하고 \(a_{y+1} - a{y}\)가 \(-z\)만큼 증가하는 것과 같다. 또, \(a_x\)를 구하기 위해서는 \((a_x - a{x-1}) + (a_{x-1} - a{x-2}) + ... + (a_1 - 0)\)를 계산해주면 되기 때문에 Fenwick Tree에서 저장하고 있는 값들을 \(1\)번째 원소 부터 \(x\)번쨰 원소까지 더해주면 된다. 따라서 구간 합 쿼리와 비슷한 방식으로 구할 수 있다.

3.1. Code

int tree[MAX_N+1];
void Update(int x, int y, int z){	// x부터 y까지 z만큼 더함
	while(x<=N){
		tree[x] += z;
		x += (x & -x);
	}
	y++;
	while(y<=N){
		tree[y] -= z;
		y += (y & -y);
	}
}

int Calc(int x){	// x번째 원소의 값을 구한다
	int ret = 0;
	while(x>0){
		ret += tree[x];
		x -= (x & -x):
	}
	return ret;
}

4. 2D Fenwick Tree

\((x, y)\) 위치에 값이 \(z\)인 2차원 구조에서 \((1, 1)\)과 \((x, y)\)를 두 꼭짓점으로 갖는 직사각형에 포함된 원소들의 구간 합을 구하는 등 쿼리를 처리하는 경우 2차원 Fenwick Tree로 해결할 수 있다. 1차원 Fenwick Tree와 비슷한 방법을 사용하므로 구현에는 어려움이 없지만, 공간 복잡도와 시간 복잡도를 잘 생각하여 사용해야 한다.

4.1. Code

int fenwick_tree[MAX_N+1][MAX_N+1];

void Update(int x, int y, int z){	// (x, y) 위치 원소가 z만큼 증가
	int ty = y;
	while(x<=N){
		y = ty;
		while(y<=N){
			fenwick_tree[y] += z;
			y += (y & -y);
		}
		x += (x & -x);
	}	
}

int Sum(int x, int y){	// (1, 1)부터 (x, y)까지 직사각형 내 원소 합
	int sum = 0, ty = y;
	while(x>0){
		y = ty;
		while(y>0){
			sum+=fenwick_tree[y];
			y -= (y & -y);
		}
		x -= (x & -x);
	}
	return sum;
}

5. Lazy Propagation in Fenwick Tree

Fenwick Tree에서 Segment Tree에서 Lazy Propagation을 해주는 것과 비슷한 연산을 구현하기는 어렵다. 대신, 다음과 같은 특수한 경우 Lazy Propagation과 같은 효과를 갖도록 해줄 수 있다.

5.1. 구간에 더하기

어떤 길이 \(N\)인 수열이 주어졌을 때, 다음 두 가지 쿼리를 처리하는 문제를 생각해보자.

Update : \(x\)번째 원소부터 \(y\)번째 원소까지 \(z\)만큼 더해준다
Sum : \(x\)번째 원소부터 \(y\)번째 원소까지 구간 합을 출력한다

Segment Tree에 Lazy Propagation을 사용하는 경우 쉽게 구할 수 있지만, Fenwick Tree를 통해 쿼리를 처리하는 방법을 살펴보자.

\(s\)부터 \(e\)까지 \(val\)만큼 더하는 경우, \(sum[i] = a[1] + a[2] + ... + a[i]\)의 변화를 관찰해 보면 \(e < i\)인 \(i\)의 경우 \(sum[i]\)가 \((e-s+1)\times val\)만큼 증가한다. \(s\leq i \leq e\)인 \(i\)의 경우 \(sum[i]\)가 \((s-i+1)\times val\)만큼 증가하며, \(i<s\)인 \(i\)에 대해서는 \(sum[i]\)에 변화가 없다.

따라서, 만약 \(i\)번째 위치의 \(sum[i]\)를 \(a_i\times i + b_i\)라 표현하면 \(s\)부터 \(e\)까지 \(val\)만큼 더하는 연산은 \(a_s\)부터 \(a_{e-1}\)까지 \(val\)만큼 더해주고 \(b_s\)부터 \(b_{e-1}\)까지 \(-val\times (s-1)\)를 더해주고 \(b_e\)부터 \(b_N\)까지 \(val\times e\)만큼 더해주는 연산으로 바뀐다.

이 \(a\)와 \(b\)값을 각각 위에서 다룬 구간 더하기 방법으로 관리하면, \(sum[i]\)를 \(a_i\)와 \(b_i\)로 구할 수 있다. 코드는 다음과 같다.

int tree1[MAX_N+1], tree2[MAX_N+1];
void Update(int x, int y, int z){ // x부터 y까지 z만큼 더하는 연산 
	int tx = x, ty = y;
	while(x<=N){
		tree1[x] += z;
		tree2[x] -= (nx-1) * z;
		x += (x & -x):
	}
	while(y<=N){
		tree1[y] -= z;
		tree2[y] += ny * z;
		y += (y & -y);
	}
}

void Sum(int x){	// 1부터 y까지 원소들 합
	int a = 0, b = 0;
	while(x>0){
		a += tree1[x];
		b += tree2[x];
		x -= (x & -x);
	}
	return a*x + b;
}

6. 관련 자료구조

Segment Tree

부모와 왼쪽 자식을 안다면 오른쪽 자식의 값도 알 수 있기 때문