_

1. 소개

최장 공통 부분 수열은 주어진 여러 개의 수열 모두의 부분 수열이 되는 수열들 중에 가장 긴 것입니다. 부분 수열은 그 수열의 일부 항을 원래 순서대로 나열해 얻을 수 있는 수열입니다. 이때 꼭 연속하지 않아도 되며, 연속한 경우는 최장 공통 문자열이라고 부릅니다.

사실 최장 공통 부분 수열은 문자를 다룰 수도 있습니다. '공통 부분 수열'과 '공통 문자열'의 차이는 연속해야 하는지의 여부입니다. 따라서 '공통 부분 수열'이 꼭 숫자로만 이루어지지 않을 수도 있습니다. 1243 은 ABDC일 수도 있고, \texttt{@^$&}일 수도 있음을 유의하시기 바랍니다.

아래와 같이 짧은 LCS는 매우 간단하므로 눈으로도 쉽게 답을 찾을 수 있습니다.

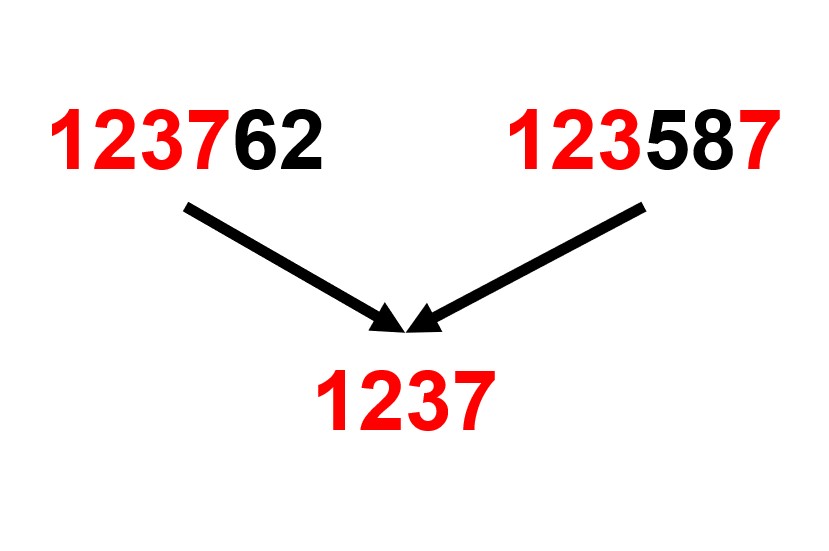
123762와 123587의 LCS를 찾아봅시다.

두 수열 모두 부분 수열로 137, 17, 237 등을 가지고 있습니다. 이때 LCS는 1237이 되고, 그 길이는 4입니다.

2. DP Table

LCS를 찾기 위한 일반적인 방법은 DP(동적계획법) Table을 만드는 것입니다.

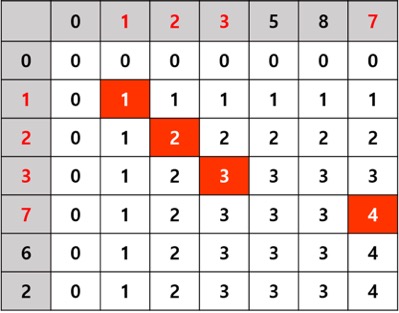
주어진 수열이 123762와 123587라고 합시다. 이 표의 가로축과 세로축은 각각의 수열을 의미합니다. 이 표에서 i번째 행,j번째 열의 수를 ARR[i][j]라 할 때 ARR[i][j]는 A를 i번째 수, B를 j번째 수 까지 고려했을 때 최장 수열의 길이입니다. 첫 번째 열과 첫 번째 행은 아직 아무 수도 고려하지 못한 상태이기 떄문에, 최장 수열의 길이는 0입니다. 0이 아닌 i, j에 대해 ARR[i][j]를 다음과 같이 정의할 수 있습니다.

if(A[i]==B[j]){
  // A[i]와 B[j]가 같은 경우
  ARR[i][j] = max(max(ARR[i-1][j], ARR[i][j-1]), ARR[i-1][j-1]+1);
}else{
  // A[i]와 B[j]가 다른 경우
  ARR[i][j] = max(ARR[i-1][j], ARR[i][j-1]);
}

만약 A[i]와 B[j]가 다르다면, 아무것도 추가할 수 없으므로 A[i]를 확인하기 전 단계인 ARR[i-1][j]와 B[j]를 확인하기 전 단계인 ARR[i][j-1] 중 더 큰 값을 저장하는 것입니다. A[i]와 B[j]가 같다면 위의 두 선택지에 더해 세 번째 선택지가 존재합니다. 두 수가 같으므로 LCS의 마지막 자리에 추가할 수 있고, 이는 두 수를 모두 고려하기 전까지의 LCS에 1을 더한 ARR[i-1][j-1] + 1입니다. 이 과정을 모두 마치고 나면 LCS의 길이는 표의 가장 마지막 위치 ARR[6][6]에 저장되어 있습니다. (A와 B가 모두 6자리이기 때문입니다.) 즉, A와 B의 모든 수를 다 고려했을 때의 LCS를 의미합니다. 만약 LCS의 길이 뿐만이 아닌 LCS 자체를 구하고 싶다면, 위 표에서 빨간색으로 채워진 칸들을 역으로 추적하면 됩니다. 위 표에서 예시를 들어 보도록 하겟습니다. 선택되었기에 빨간색이 칠해진 칸들을 보면 모두 공통점이 있습니다. 같은 숫자를 가진 칸들 중 가장 왼쪽 위의 칸이라는 것입니다. 이것은 전 칸에서 넘어올 때 길이가 1 늘었다는 뜻이고, 그 칸이 LCS에 포함된다는 뜻입니다. 따라서 LCS를 구하려면, 끝에서 시작해 왼쪽이나 위에 같은 수가 있으면 그곳으로 가고, 왼쪽 칸과 윗칸이 모두 자신보다 작다면 자신을 LCS에 추가한 후 왼쪽 위에 있는 칸으로 가면 됩니다.

3. Code

지금까지 설명한 내용이 그대로 담겨 있는 문제가 있습니다. 따라서 구현 코드와 문제 설명을 같이 하겠습니다. 이 문제는 두 문자열을 입력받은 후, LCS의 길이와 LCS를 출력하는 문제입니다.

#include <bits/stdc++.h>
using namespace std;
char A[1010], B[1010], LCS[1010];
int DP[1010][1010], LEN;
int main() {
    scanf("%s", A + 1);
    scanf("%s", B + 1);
    
    // strlen()의 이용을 위해
    // A[0]과 B[0]에 임의의 문자를 입력
    A[0] = B[0] = '.';
    
    // lenA와 lenB는 각각 A와 B의 길이
    int lenA = strlen(A) - 1, lenB = strlen(B) - 1;
    
    for(int i = 1; i <= lenA; i++) {
        for(int j = 1; j <= lenB; j++) {
            if(A[i] == B[j])
                // A[i]와 B[j]가 같아서
                // LCS를 늘릴 수 있는 경우
                DP[i][j] = max(DP[i - 1][j - 1] + 1, max(DP[i - 1][j], DP[i][j - 1]));
            else
                // 다른 경우
                DP[i][j] = max(DP[i - 1][j], DP[i][j - 1]);
        }
    }
    
    LEN = DP[lenA][lenB];
    
    //LCS의 길이 출력
    printf("%d\n", LEN);
    
    int a = lenA, b = lenB;
    
    while(LEN > 0) {
        if(DP[a][b] == DP[a - 1][b]) {
            // DP[a][b]가 색칠되지 않은 경우
            a--;
        }
        else if(DP[a][b] == DP[a][b - 1]) {
            // DP[a][b]가 색칠되지 않은 경우
            b--;
        }
        else {
            // DP[a][b]가 색칠되었고 LCS에 해당하는 경우
            
            // A[a]와 B[b]중 어떤 것을 써도 상관없다.
            LCS[LEN - 1] = A[a];
            a--;
            b--;
            LEN--;
        }
    }
    
    //LCS 출력
    printf("%s\n", LCS);
}