_
1. 소개
LCA(Lowest Common Ancestor)는 트리에서 두 노드 \(v\)와 \(w\)의 가장 낮은 공통 조상으로, \(v\)와 \(w\)를 모두 자손으로 갖는 노드들 중에서 가장 루트에서 먼 노드를 말한다. Sparse Table을 사용하여 LCA를 \(O(\log N)\)에 구할 수 있다.
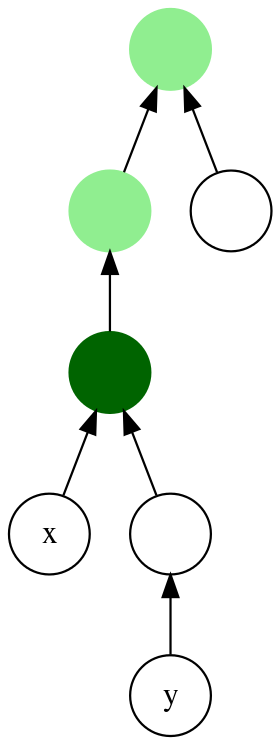
위 그림에서 초록색 정점들이 \(x\)와 \(y\)의 공통 조상이며, 그 중에서 진한 초록색 정점이 LCA다.
2. Code
void dfs(int x){
up[x][0] = p[x]; // x에서 2^0(= 1)번 올라가면 p[x](x의 부모 노드)
for(int j=1; j<MAX_K; j++){ // MAX_K = log(N)번 반복
//up[x][j]에 x에서 2^j번 올라간 노드 번호를 저장해준다
up[x][j] = up[up[x][j-1]][j-1];
}
for(int next : gp[x]){
if(next==p[x]) continue; // next가 x의 부모인 경우
p[next] = x;
lv[next] = lv[x]+1; // 다음 노드의 level을 계산해준다
dfs(next);
}
}
int lca(int x, int y){
for(int i=MAX_K-1; i>=0; i--){
// x와 y의 level이 일치할 때까지 level이 높은 노드의 level을 줄인다
if(lv[up[x][i]]>=lv[y]) x = up[x][i];
if(lv[up[y][i]]>=lv[x]) y = up[y][i];
}
if(x==y) return x;
for(int i=MAX_K-1; i>=0; i--){
if(up[x][i]!=up[y][i]){
x = up[x][i];
y = up[y][i];
}
}
return up[x][0];
}