_

1. Day 1

1.1. 1. Comparing Plants

1.2. 2. Connecting Supertrees

문제

1.2.1. 문제 설명

• N개의 정점이 있다
• 정점 i에서 정점 j로 가는 서로 다른 단순경로가 정확히 p(i, j)개가 되도록 그래프를 설계할 것이다. (\(0 \leq p(i, j) \leq 3\))
• 이를 만족하는 그래프가 존재하는지 판별하고, 존재한다면 그 중 하나를 구하여라.

1.2.2. 존재성 판별

• 일단, 조건을 만족하는 그래프가 존재하는지부터 생각해보자.
• 96점까지는 0 ≤ p(i, j) ≤ 2이므로, 0 ≤ p(i, j) ≤ 2일 때를 생각해보자.
  • p(x, y) = 1에 대한 관찰
    • 정점 i에 대하여 p(x, y) = 1인 j들의 집합을 S라 하자.
    • 그러면 x, y ∈ S인 모든 x, y에 대하여, p(x, y) = 1이다.
      • pf) p(x, y) ≠ 0임은 자명하다. (x``i``y 경로가 존재하므로 x``y 단순경로도 존재) p(x, y) = 2인 (x, y)가 존재한다고 가정하자.
        1. i``x``y 단순경로인 경우 p(i, y)=2인데, S의 정의에 의하여 모순이다.
        2. x``i``y 단순경로인 경우 x``i 경로와 i``y 경로가 유일하므로, p(x, y) = 2인 것이 불가능하다.
    • 또한, x, y ∈ S인 모든 x, y와 임의의 정점 k에 대하여 p(x, k) = p(y, k)이다.
    • 따라서, 이러한 집합 S에 대하여, S의 원소들을 일직선의 체인 형태로 이어주고, S의 원소 중 임의의 하나를 잡아서 그 하나의 정점에 대해서만 S 외부의 정점과 간선을 이어주면 된다.
  • p(i, j) = 2에 대한 관찰
    • 이제 p(i, j) = 1인 (i, j)는 존재하지 않는다.
    • 정점 i에 대하여 p(i, j) = 1인 j들의 집합을 T라 하자.
    • 그러면 x, y ∈ T인 모든 x, y에 대하여, p(x, y) = 2이다.
      • pf) T의 원소들은 하나의 컴포넌트에 존재하므로 p(x, y) = 0인 (x, y)는 존재하지 않는다.
    • 따라서, 이러한 집합 T에 대하여, T의 모든 원소들을 하나의 사이클 형태로 이어주면 된다.
• 따라서, 앞에서 정의한 집합 S, T에 대하여 다음 조건을 모두 만족하는지 확인한다면 주어진 입력의 조건에 맞는 그래프를 설계할 수 있는지 판별할 수 있다.
  • x, y ∈ S인 모든 x, y에 대하여, p(x, y) = 1
  • x, y ∈ T인 모든 x, y에 대하여, p(x, y) = 2

1.2.3. 그래프 설계

결과적으로, 앞에서 설명한 것과 같이 그래프를 설계하면, 결과 그래프는 다음과 같이 여러 개의 ‘하나의 컴포넌트에 최대 하나의 사이클이 존재하는 선인장 그래프’ 로 나타낼 수 있다.

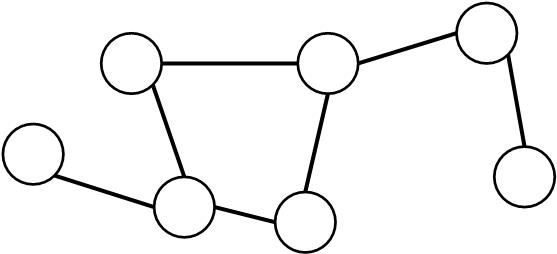
1.2.4. p(i, j) = 3 ?

• 결과적으로 말하면, p(i, j) = 3인 (i, j)가 존재하는 경우 답은 존재하지 않는다.

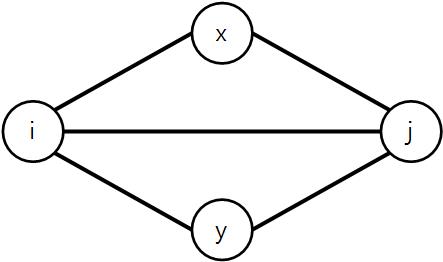
• 위는 p(i, j) = 3을 만족하게 만든 그래프이다. 위와 같이, i에서 j로 가는 같은 단순 경로 위에 존재하지 않는 두 정점 x, y가 존재하게 된다.
• 이 경우, p(x, y) > 3 (x``i``y, x``j``y, x``i``j``y, x``j``i``y)가 되기 때문에, p(i, j) = 3인 (i, j)가 존재하는 경우 조건을 만족하는 그래프는 존재하지 않는다.

1.3. 3. Carnival Tickets

문제

1.3.1. 문제 설명

• n가지 색의 티켓이 각 색마다 m개씩 존재하며, 티켓에는 각각 하나의 정수가 쓰여있다.
• k회의 라운드마다, 하나의 색에서 하나의 카드를 선택하여 카드에 대해 점수를 받는다. 뽑은 카드에 적힌 숫자들을 크기 순서대로 \(A_{1}, A_{2}, ... , A_{m}\)이라고 하자. 마스터 또한 카드 한장을 뽑는다. 마스터가 뽑은 카드에 적힌 수가 b라고 하면, \(\sum |A_{i}-b|\)이 이번 라운드에 얻게 되는 점수이다.
• 각 라운드가 끝날때 마다 라운드에서 사용된 카드는 버려진다.
• 마스터는 각 라운드마다 점수가 최소화되도록 b를 선택한다.
• 가장 많은 점수를 얻을 수 있도록 각 라운드마다 고르는 카드를 선택하자.

1.3.2. 필요한 관찰

• 각 라운드에는 획득하는 점수는 정확히 얼마인가?
  • 뽑은 카드에 적힌 숫자들을 크기 순서대로 \(A_{1}, A_{2}, ... , A_{n}\)이라고 하자.
  • 마스터가 항상 최적의 b를 선택한다면, 획득하는 점수는 \(S = A_{n}+A_{n-1}+...+A_{n/2+1}-A_{n/2}-...-A_{2}-A_{1}\)이 된다.

1.3.3. 티켓 선택

• 전체 티켓 \(nm\)개 중, 점수가 더해지는 티켓 \(nk/2\)개와, 점수가 차감되는 티켓 \(nk/2\)개를 고르게 된다. 이상 점수가 더해지는 티켓을 P 티켓, 차감되는 티켓을 Q 티켓이라 부르겠다.
• 또한, 한 종류의 색에서는 정확히 k개의 티켓을 골라야 한다.
• 어떻게 고를 것인가?
  • 점수의 초기값은 \(\sum_{i=0}^{n-1} \sum_{j=0}^{k-1} x(i, j)\)로 놓자. (처음에는 모든 티켓이 Q티켓)
  • 이제 Q 티켓 중 \(nk/2\)개를 P 티켓으로 교체해야 한다.
  • 우선 max heap에 \(x(i, k-1)+x(i, m-1)\)들을 모두 추가한다.
  • 다음의 과정을 \(nk/2\)회 반복한다:
    1. max heap에서 최댓값을 확인한다.(이를 \(x(i, j)+x(i, j+m-k)\)라고 하자.) 이것의 의미는, Q 티켓에서 \((i, j)\) 티켓을 삭제하고, P 티켓에 \((i, j+m-k)\) 티켓을 추가한다는 뜻이다.
    2. 확인한 최댓값을 S에 더해주고 pop한다.
    3. max heap에 \(x(i, j-1)+x(i, j+m-k-1)\)을 추가한다. 만약 \(j = 0\)이라면, 색 i에서 k개의 티켓을 전부 확정한 것이기 때문에 추가하지 않는다.
  • 위의 프로세스로 티켓을 고르는 것은
    • 한 종류의 색 당 k개의 티켓 선택
    • 총 P 티켓의 개수와 Q 티켓의 개수가 각각 \(nk/2\) 의 조건을 만족하도록 티켓을 고른 경우 중 점수가 최대가 되는 경우임이 자명하다.
  • 또한, P 티켓 중 최솟값은 Q 티켓 중 최댓값보다 항상 크다. 만약 아니라면, 해당 두 티켓을 바꿔주면 S가 증가하게 되므로 모순이다.

1.3.4. 티켓 배치

• 이제 티켓을 배치하여야 한다. 앞에서와 같이 티켓을 고르면 항상 티켓을 배치하는 방법이 있을까?
• 있다.
  • 색 i의 티켓 중 P 티켓의 수를 \(P_{i}\)라고 하자.
  • 각 라운드에서는 \(P_{i}\)가 큰 순서대로 \(n/2\)개의 색을 골라서 이 색들에서 P 티켓을 뽑고, 나머지 색은 Q 티켓을 뽑는다.
  • 이후, 사용한 티켓을 삭제한다. \(P_{i}\)도 같이 갱신한다.
  • 이렇게 배치하면 항상 한 라운드에 \(n/2\)개의 P 티켓과 Q 티켓을 각 색에서 하나씩 배치할 수 있다. 이는 비둘기집의 원리에 의하여 간단하게 증명할 수 있다.

2. Day 2

2.1. 1. Packing Biscuits

2.1.1. 문제 설명

• k 종류의 비스킷이 있다.
  • i번 비스킷의 맛 점수는 \(2^i\)이다.
  • i번 비스킷은 \(a_i\)개가 있다.
• x개의 가방에 비스킷을 배분하여야 한다.
  • 모든 가방에 담긴 i번 비스킷의 개수의 합은 \(a_i\)를 넘길 수 없다.
  • 한 가방에 담긴 모든 비스킷의 맛 점수의 합을 가방의 총 맛이라고 했을 때, 모든 가방의 총 맛은 전부 y로 동일해야 한다.
• 쿼리로 x가 주어질 때, 가능한 y의 개수를 구하여라.

2.1.2. Subtask #2, #3

• 쿼리의 개수가 매우 작다.
• y를 작은 비트부터 확인하자.
• DP(i, j) = (y의 i번째 비트를 볼 때, 이전 단계에서 남은 비스킷 i가 j개 있는 경우 가능한 y의 경우의 수) 라고 정의하자.
• \(DP(i, j) = \sum_{k=0}^x DP(i+1, \lfloor {{j+A_i-k} \over 2} \rfloor)\)
• i에 대하여 가능한 j가 [a, a+x] 범위에서 나타난다면, \( \lfloor {{j+A_i-k} \over 2} \rfloor\)은 \( \left[ {{a+A_i-x} \over 2} , {{a+A_i+x} \over 2} \right] = \left[ {{a+A_i-x} \over 2} , {{a+A_i-x} \over 2} + x \right] \) 범위에서 나타나게 되어 j의 최댓값과 최솟값의 차가 x로 유지된다.
• 따라서, map이나 unordered_map 등을 이용해서 구현해준다면 \(O(KX \log K)\) 또는 \(O(KX \log K \log X ) \) 정도의 시간복잡도로 구현할 수 있다.

2.1.3. Full Solution

• 앞에서와 같이 DP(i, j)로 두 개의 인자를 관리한다면 \(O(KX)\) 이하로 줄이기 힘들다.
• 다음과 같이 새롭게 DP 배열을 정의하자.
  • DP[i] = i번 비스킷까지 사용했을 때 만들 수 있는 y의 경우의 수
• 이 때, 다음과 같은 점화식을 세울 수 있다.
  • y’ = i번 비스킷까지 사용했을 때 만들 수 있는 최대 y라고 했을 때, \( DP[i] = \sum_{(1<<j)y'\ = \ true인\ 모든\ j DP[j] + 1 \)
• 예) i=5, j=23
  • DP[4] : y가 0xxxx(2) 꼴인 경우
  • DP[2] : y가 100xx(2) 꼴인 경우
  • DP[1] : y가 1010x(2) 꼴인 경우
  • DP[0] : y가 10110(2) 꼴인 경우
  • 1 : y가 10111(2)인 경우
• 최종 시간복잡도는 \(O(K^2)\) 이다.

2.2. 2. Counting Mushrooms

2.3. 3. Stations