_

1. 소개

일반적으로 배열에서의 탐색은 전 탐색 시에 $O(N)$, 정렬하고 이분 탐색 시에 $O(\log N)$ 으로 처리 가능합니다. 그러나, 어떤 경우에는 이러한 시간복잡도로도 부족하여서, 또는 정렬하고 이분 탐색하는 것이 불가능할 때 해싱이라는 기법을 사용합니다. 해싱이란 데이터의 효율적인 관리를 위하여 임의의 길이의 데이터를 고정된 길이의 데이터로 변환하여 처리하는 과정입니다. 해싱은 크게 두 개의 부분으로 이루어지는데, 그것은 해시 테이블과 해시 함수입니다.

2. Hash Table

일반적인 자료구조를 사용하면 위에서 말했듯이, 하나의 원소를 탐색하는데 최소 $O(\log N)$의 시간이 필요하게 됩니다. 이를 해시 테이블을 이용하여 시간을 줄일 수 있습니다. 해시 테이블은 공간을 담보로 시간을 사는 자료구조입니다. 데이터를 해시 함수에 넣어서 나온 주소에 데이터를 저장하게 되는데, 이때 데이터로 채워지지 않은 공간이 많아야 해시 테이블이 뒤에서 다룰 해시 충돌을 일으키지 않기 때문입니다.

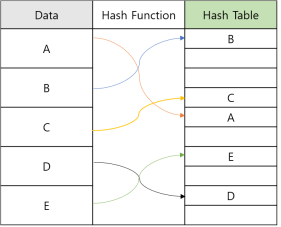
3. Hash Function

해시 함수는 가지고 있는 데이터를 해시 테이블 내의 주소로 변환하는 함수입니다. 이 해시 함수는 해싱 과정 전체에서 매우 중요한 역할을 맡습니다. 해시 함수를 잘 짜야 해시 충돌이 일어나지 않고, 이론적인 성능에 더 가까워지기 때문입니다. 다음은 가장 흔히 알려진 해시 함수들입니다.

3.1. 나눈셈법

가장 기본적인 해시 함수입니다. 주어진 데이터를 integer 값으로 변환한 뒤, 그 integer 값을 해시 테이블의 전체 크기로 나누는 방식입니다. $$ Index = data % size $$

C++ STL의 unordered_map과 unordered_set도 이와 같은 나눗셈법을 사용한다고 합니다.

int HashFunction(int Key, int TableSize){
	return Key%TableSize;
}

3.2. 곱셈법

Key가 실수이고 $0 \leq A \le 1$인 A에 대하여, 곱셈법은 다음과 같이 정의합니다.

$$ Hash(Key) = {KeyA} \times TableSize $$ 단, {x}는 x의 소수 부분의 값이다. TableSize는 중요하지는 않지만, 이진법 연산을 하는 컴퓨터의 특성상 2의 거듭제곱을 사용하는 것이 살짝 더 빠릅니다.

int HashFunction(double Key, int TableSize){
	double d=(double)((int)Key);
	return (int)((Key-d)*TableSize);
}

3.3. 문자열

문자열을 해싱하기 위해 정수로 바꾸는 방법은 여러 가지가 있지만, 가장 흔히 쓰이는 방법은 다음과 같습니다.

long long HashFunction(char * Key, int KeyLen, int TableSize){
	long long val=0 ;
	int Prime[]={/*해싱에 사용되는 소수들의 배열*/}
	for (int i=0 ; i<KeyLen; i++)
    val+=Prime[Key[i]];	//val 값을 TableSize에 맞게 해싱해준다.
	return val;
}

3.4. Universal Method

유니버설 해싱은 다음의 특성을 가지는 해시 함수를 선택하기 위한 확률적 알고리즘입니다. 어떤 두 개의 서로 다른 데이터 x, y에 대하여 x 와 y 간에 해시 충돌이 발생할 확률, 다시 말해 F(x)=F(y)일 확률이 F가 랜덤 함수일 확률과 같다. 따라서, F가 정의역의 크기가 r인 함숫값을 가질 때, 특정 해시 충돌이 발생할 확률은 최대 $r^{-1}$과 같다. 이 Universal Method는 특정 함수가 아닌, 위와 같은 조건을 만족하는 함수를 통틀어서 지칭하는 기법입니다. 따라서 다양한 함수들이 Universal Method의 조건을 만족할 수 있습니다.

4. Hash Collision

해시 충돌은 해시 함수가 중요한 이유입니다. 해시 충돌이란 서로 다른 데이터가 동일한 해시값을 가지게 되어 해시 테이블에서 인덱스가 겹치게 되는 경우입니다. 해시 충돌이 일어나는 경우, 해시 충돌을 처리하는 과정에서 시간이 소모되므로 해시 테이블이 이론적인 성능을 내지 못하게 됩니다. 따라서 해시 충돌이 일어날 때의 해시 테이블에서의 처리도 중요하지만, 해시 충돌 자체가 적게 일어나도록 해시 함수 자체를 해시 충돌이 일어날 확률이 적게 만들어야 합니다. 해시 충돌을 해시 테이블에서 처리하는 방법은 여러 가지가 있습니다. 대표적으로는 해시 충돌이 일어났을 때 해당 인덱스에 Linked List를 만들어서 처리하는 방법이나, 다른 인덱스로 넘어가서 데이터를 저장하는 방법 등이 있습니다. 전자는 해당 인덱스의 원소 개수만큼의 시간복잡도를 소모하지만 다른 인덱스에 간섭을 안하고, 후자는 다음으로 나오는 빈 인덱스까지의 거리 만큼의 시간복잡도만 소모하지만 다른 인덱스를 차지하게 되어 해당 인덱스를 해시값으로 가지는 데이터의 탐색 시간까지 늘려버릴 수 있습니다. 이처럼, 해시 충돌이 일어나게 되면 극단적이면 전탐색과 비슷한 시간복잡도가 나올 수 있으므로 해시 함수 자체에서 해시 충돌을 방지하는 코드를 짜는 것이 좋습니다.

5. 예제

구간 성분(KOI 2015 고등부 2번)

이 문제는 $S_A$와 $S_B$내의 구성 성분이 같은 가장 긴 부분 문자열의 길이를 구하는 문제입니다.

일단 단순하게 생각한다면 길이가 같은 $S_A$와 $S_B$의 부분 문자열을 서로 모두 비교해 보는 방식으로 $O(N^4)$으로 구할 수 있습니다. Time Limit이 1000ms이므로 이를 통해 부분문제 1을 통과할 수 있습니다.

Set이나 Map 등의 $O(\log N)$만에 탐색을 해주는 자료구조에 $S_A$의 구간성분을 저장한 26칸짜리 배열을 넣어주어서 $S_B$의 구간성분과 비교하여 준다면 시간복잡도 자체는 $O(N^2\log N)$이 되지만, 상수로 26이 붙게 되므로 부분문제 2만을 추가적으로 통과하게 됩니다.

해싱을 적용하여 $O(\log N)$만에 탐색을 해주는 자료구조에 의 각 구간의 구간성분을 해싱하여 넣어준다면, 의 각 구간의 구간성분이 Table에 존재하는지 $O(\log N)$만에 확인이 가능합니다. 또한, 구간성분의 길이가 바뀔 때마다 초기화를 해준다면 최대 long long 크기의 integer 1500개만을 자료구조에 저장하게 되므로 ML도 넉넉하게 만족하게 됩니다. 따라서 전체 시간복잡도는 $O(N^2\log N)$이 되어, 간단하게 부분문제 3, 4를 통과하게 됩니다.

6. 여담

해싱은 Problem Solving 이외에도 해시값과 원본 데이터 사이의 관계가 없다는 점을 이용하여 보안에 널리 이용됩니다. 특히 최근 비트코인 등으로 인해 화제가 되었던 암호화폐에 적용되는 위변조 방지 기술인 ‘블록체인’에 사용됩니다. 사실 해싱은 PS보다는 실제 개발 등에서 많이 쓰이는 기법이지만, 해싱 이외의 풀이로는 TLE나 MLE가 나는 문제에서 시간, 공간 복잡도를 줄이기에 좋은 방법이 될 수 있습니다.